Vracející se kombinace
Pomocí číselné tabulky nebo CTE generujícího čísla vyberte 0 až 2^n - 1. Pomocí bitových pozic obsahujících 1s v těchto číslech označte přítomnost nebo nepřítomnost relativních členů v kombinaci a eliminujte ty, které nemají správný počet hodnot, měli byste být schopni vrátit sadu výsledků se všemi požadovanými kombinacemi.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Tento dotaz funguje docela dobře, ale vymyslel jsem způsob, jak jej optimalizovat, cribbing z Nifty Parallel Bit Count nejprve získat správný počet položek odebraných najednou. To funguje 3 až 3,5krát rychleji (jak CPU, tak čas):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Šel jsem si přečíst stránku počítání bitů a myslím si, že by to mohlo fungovat lépe, kdybych neprováděl % 255, ale šel celou cestu s bitovou aritmetikou. Až budu mít příležitost, zkusím to a uvidím, jak to bude fungovat.
Moje nároky na výkon jsou založeny na dotazech spuštěných bez klauzule ORDER BY. Pro upřesnění, co tento kód dělá, je počítání počtu nastavených 1 bitů v Num z Numbers stůl. Je to proto, že číslo se používá jako jakýsi indexátor k výběru prvků sady v aktuální kombinaci, takže počet 1 bitů bude stejný.
Doufám, že se vám to líbí!
Pro záznam, tato technika použití bitového vzoru celých čísel k výběru členů množiny je to, co jsem vytvořil jako "Vertical Cross Join". Účinně vede k křížovému spojení více sad dat, kde je počet sad a křížových spojení libovolný. Počet sad je zde počet položek pořízených najednou.
Ve skutečnosti křížové spojení v obvyklém horizontálním smyslu (přidání dalších sloupců do existujícího seznamu sloupců s každým spojením) by vypadalo asi takto:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Moje výše uvedené dotazy efektivně "křížové spojení" tolikrát, kolikrát je potřeba, pouze s jedním spojením. Výsledky jsou neotočné ve srovnání se skutečnými křížovými spoji, jistě, ale to je nepodstatná záležitost.
Kritika vašeho kodexu
Za prvé, mohu navrhnout tuto změnu vašemu Factorial UDF:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Nyní můžete vypočítat mnohem větší sady kombinací a navíc je to efektivnější. Můžete dokonce zvážit použití decimal(38, 0) abyste ve svých kombinačních výpočtech umožnili větší mezivýpočty.
Za druhé, váš zadaný dotaz nevrací správné výsledky. Například při použití mých testovacích dat z níže uvedeného testování výkonu je sada 1 stejná jako sada 18. Zdá se, že váš dotaz má klouzavý pruh, který se obtáčí:každá sada má vždy 5 sousedních členů a vypadá asi takto (otočil jsem aby bylo lépe vidět):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Porovnejte vzor z mých dotazů:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Abychom pro každého, koho to zajímá, dostali bitový vzor -> index kombinace, všimněte si, že 31 v binárním tvaru =11111 a vzor je ABCDE. 121 v binární podobě je 1111001 a vzor je A__DEFG (zpětně mapovaný).
Výsledky výkonu s tabulkou reálných čísel
U druhého výše uvedeného dotazu jsem provedl nějaké testování výkonu s velkými sadami. V tuto chvíli nemám záznam o použité verzi serveru. Zde jsou moje testovací data:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter ukázal, že toto „vertikální křížové spojení“ nefunguje tak dobře jako jednoduché psaní dynamického SQL, aby skutečně provedlo křížové spojení, kterému se vyhýbá. Za triviální cenu několika dalších čtení má jeho řešení metriky 10 až 17krát lepší. Výkon jeho dotazu klesá rychleji než můj s přibývajícím množstvím práce, ale ne dostatečně rychle, aby to někomu zabránil v jeho používání.
Druhá sada čísel níže je faktor dělený prvním řádkem v tabulce, aby bylo vidět, jak se mění.
Erik
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Petře
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Extrapoluji, nakonec bude můj dotaz levnější (i když je od začátku ve čtení), ale ne na dlouhou dobu. Chcete-li použít 21 položek v sadě již vyžaduje tabulku čísel až do 2097152...
Zde je komentář, který jsem původně učinil, než jsem si uvědomil, že moje řešení by fungovalo výrazně lépe s průběžnou tabulkou čísel:
Výsledky výkonu s průběžnou tabulkou čísel
Když jsem původně napsal tuto odpověď, řekl jsem:
No, zkusil jsem to a výsledky byly, že to fungovalo mnohem lépe! Zde je dotaz, který jsem použil:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Všimněte si, že jsem vybral hodnoty do proměnných, abych zkrátil čas a paměť potřebnou k testování všeho. Server stále dělá stejnou práci. Upravil jsem Petrovu verzi, aby byla podobná, a odstranil jsem zbytečné doplňky, aby byly obě co nejštíhlejší. Verze serveru použitá pro tyto testy je Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) běžící na virtuálním počítači.
Níže jsou grafy znázorňující výkonnostní křivky pro hodnoty N a K do 21. Základní údaje pro ně jsou v další odpověď na této stránce . Hodnoty jsou výsledkem 5 spuštění každého dotazu pro každou hodnotu K a N, po kterých následuje vyhození nejlepší a nejhorší hodnoty pro každou metriku a zprůměrování zbývajících 3.
V zásadě má moje verze „rameno“ (v levém rohu grafu) při vysokých hodnotách N a nízkých hodnotách K, díky kterým tam funguje hůře než dynamická verze SQL. To však zůstává poměrně nízké a konstantní a centrální vrchol kolem N =21 a K =11 je mnohem nižší pro dobu trvání, CPU a čtení než dynamická verze SQL.
Přiložil jsem graf počtu řádků, u kterých se očekává, že každá položka vrátí, abyste viděli, jak si dotaz vede v porovnání s tím, jak velkou práci musí udělat.
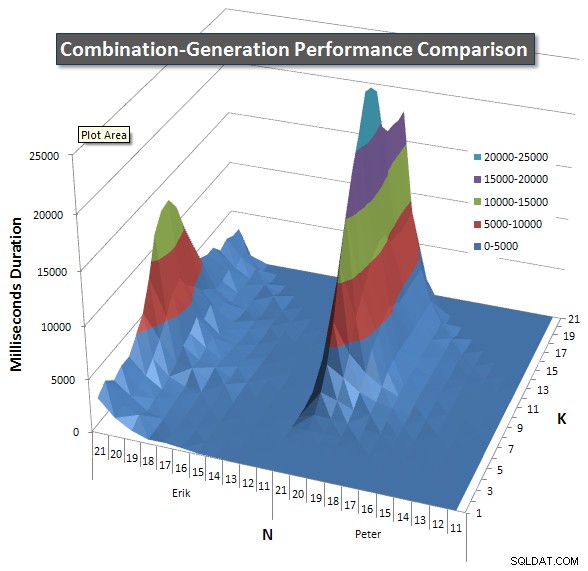
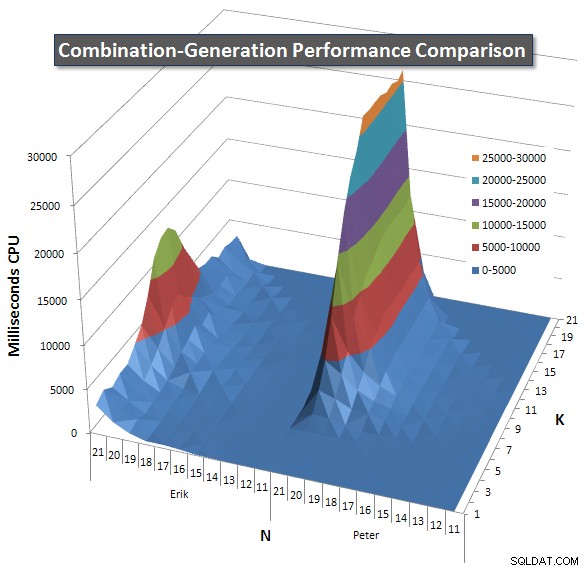
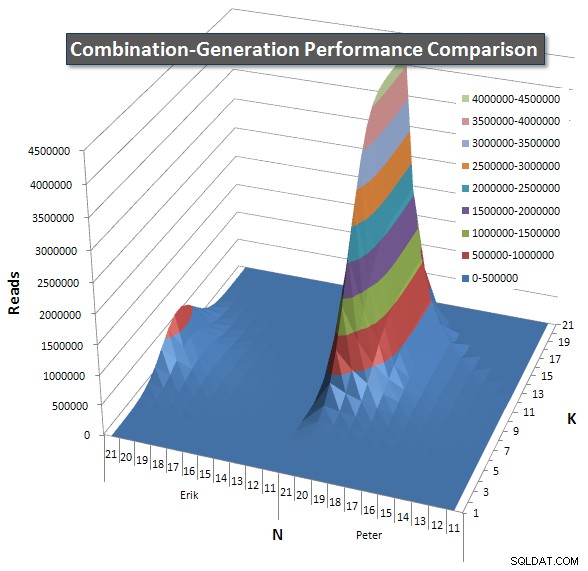
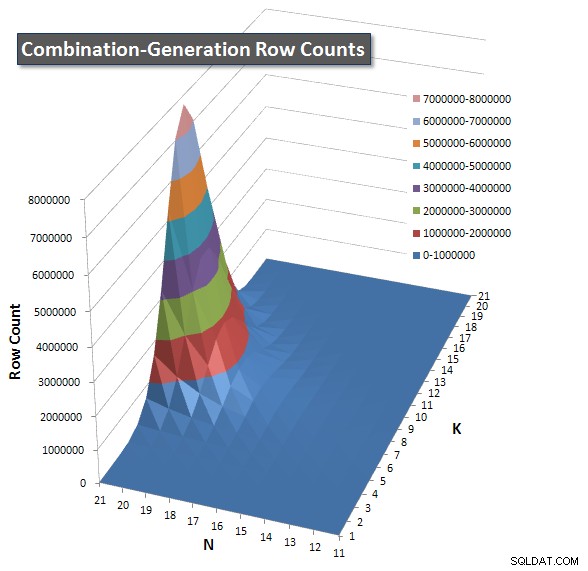
Přečtěte si prosím moji další odpověď na této stránce pro kompletní výkonnostní výsledky. Dosáhl jsem limitu počtu znaků příspěvku a nemohl jsem to sem zahrnout. (Nějaké nápady, kam to zařadit?) Abych uvedl věci do souladu s výsledky výkonu mé první verze, zde je stejný formát jako předtím:
Erik
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Petře
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Závěry
- Tabulky čísel za běhu jsou lepší než skutečné tabulky obsahující řádky, protože čtení jedné při velkém počtu řádků vyžaduje hodně I/O. Je lepší použít trochu CPU.
- Moje počáteční testy nebyly dostatečně široké, aby skutečně ukázaly výkonnostní charakteristiky obou verzí.
- Peterovu verzi lze vylepšit tím, že každý JOIN bude nejen větší než předchozí položka, ale také omezí maximální hodnotu podle toho, kolik dalších položek se musí do sady vejít. Například u 21 položek pořízených 21 najednou existuje pouze jedna odpověď o 21 řádcích (všech 21 položek najednou), ale mezilehlé sady řádků v dynamické verzi SQL, na začátku plánu provádění, obsahují kombinace jako " AU" v kroku 2, i když to bude při příštím spojení zahozeno, protože není k dispozici žádná hodnota vyšší než "U". Podobně bude mezilehlá sada řádků v kroku 5 obsahovat "ARSTU", ale jedinou platnou kombinací v tomto okamžiku je "ABCDE". Tato vylepšená verze by neměla nižší vrchol ve středu, takže by se možná nezlepšila natolik, aby se stala jasným vítězem, ale stala by se alespoň symetrickou, takže grafy by nezůstaly na maximu za středem regionu, ale klesly by zpět. k téměř 0 jako moje verze (viz horní roh vrcholů pro každý dotaz).
Analýza trvání
- Mezi verzemi není žádný skutečně významný rozdíl v trvání (>100 ms), dokud nebude 14 položek pořízeno po 12 najednou. Do této chvíle moje verze vyhrála 30krát a dynamická verze SQL vyhrála 43krát.
- Od 14-12 byla moje verze rychlejší 65krát (59>100 ms), dynamická verze SQL 64krát (60>100 ms). Nicméně pokaždé, když byla moje verze rychlejší, ušetřila celkovou průměrnou dobu trvání 256,5 sekund, a když byla dynamická verze SQL rychlejší, ušetřila 80,2 sekund.
- Celková průměrná doba trvání všech pokusů byla Erikovi 270,3 sekund, Petrovi 446,2 sekund.
- Pokud byla vytvořena vyhledávací tabulka pro určení, kterou verzi použít (výběrem rychlejší verze pro vstupy), všechny výsledky by bylo možné provést za 188,7 sekund. Použití nejpomalejšího by pokaždé trvalo 527,7 sekund.
Analýza čtení
Analýza trvání ukázala, že můj dotaz vyhrál o významné, ale ne příliš velké množství. Když se metrika přepne na čtení, objeví se velmi odlišný obrázek – můj dotaz používá v průměru 1/10 čtení.
- Neexistuje žádný skutečně významný rozdíl mezi verzemi v přečtení (>1000), dokud není 9 položek odebráno 9 najednou. Do této chvíle moje verze vyhrála 30krát a dynamická verze SQL vyhrála 17krát.
- Od 9.–9. má moje verze spotřebovala méně čtení 118krát (113>1000), dynamická verze SQL 69krát (31>1000). Nicméně pokaždé, když moje verze používala méně čtení, ušetřila v průměru 75,9 milionů čtení, a když byla dynamická verze SQL rychlejší, ušetřila 380 tisíc čtení.
- Celkový průměr čtení pro všechny pokusy byl Erik 8,4 milionů, Peter 84 milionů.
- Pokud by byla vytvořena vyhledávací tabulka k určení, kterou verzi použít (výběrem té nejlepší pro vstupy), mohly by být všechny výsledky provedeny při 8 milionech čtení. Pokaždé použití nejhoršího by zabralo 84,3 milionů čtení.
Velmi by mě zajímaly výsledky aktualizované dynamické verze SQL, která klade zvláštní horní limit na položky vybrané v každém kroku, jak jsem popsal výše.
Dodatek
Následující verze mého dotazu dosahuje zlepšení o přibližně 2,25 % oproti výše uvedeným výsledkům výkonu. Použil jsem metodu počítání bitů HAKMEM MIT a přidal jsem Convert(int) na výsledku row_number() protože to vrací bigint. Samozřejmě bych si přál, aby to byla verze, se kterou jsem používal pro všechna výše uvedená výkonnostní testování a grafy a data, ale je nepravděpodobné, že ji někdy zopakuji, protože to bylo pracné.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
A nemohl jsem odolat a ukázat ještě jednu verzi, která provádí vyhledávání pro získání počtu bitů. Může být dokonce rychlejší než jiné verze:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))
