Odhad spojení SQL Server pomocí hrubého zarovnání histogramu

Primární změny provedené v odhadu mohutnosti počínaje vydáním SQL Server 2014 jsou popsány v dokumentu Microsoft White Paper Optimalizace vašich plánů dotazů pomocí nástroje SQL Server 2014 Cardinality Estimator od Joe Sacka, Yi Fanga a Vassilise Papadimose.

Jedna z těchto změn se týká odhadu jednoduchých spojení s jediným predikátem rovnosti nebo nerovnosti pomocí statistických histogramů. V části nazvané „Připojit změny odhadovaného algoritmu“ článek představil koncept „hrubého zarovnání“ pomocí minimálních a maximálních hranic histogramu:

Přestože je starší CE potenciálně méně konzistentní, může produkovat o něco lepší odhady podmínek jednoduchého spojení kvůli postupnému zarovnání histogramu. Nový CE používá hrubé zarovnání. Rozdíl v odhadech však může být dostatečně malý, takže bude méně pravděpodobné, že způsobí problém s kvalitou plánu.

Jako jeden z technických recenzentů tohoto článku jsem cítil, že by bylo užitečné trochu více podrobností o této změně, ale to se nedostalo do konečné verze. Tento článek přidává některé z těchto podrobností.

Příklad zarovnání hrubého histogramu

hrubé zarovnání příklad v dokumentu White Paper používá verzi Data Warehouse ukázkové databáze AdventureWorks. Navzdory názvu je databáze poměrně malá; záloha má pouze 22,3 MB a rozšíří se na přibližně 200 MB. Lze jej stáhnout prostřednictvím odkazů na stránce dokumentace instalace a konfigurace AdventureWorks.

Dotaz, který nás zajímá, se připojí k FactResellerSales a FactCurrencyRate tabulky.

SELECT
    FRS.ProductKey,
    FRS.OrderDateKey,
    FRS.DueDateKey,
    FRS.ShipDateKey,
    FCR.DateKey,
    FCR.AverageRate,
    FCR.EndOfDayRate,
    FCR.[Date]
FROM dbo.FactResellerSales AS FRS
JOIN dbo.FactCurrencyRate AS FCR
    ON FCR.CurrencyKey = FRS.CurrencyKey;

Toto je jednoduché ekvijoin na jednom sloupci takže se kvalifikuje pro odhad mohutnosti spojení a selektivity pomocí hrubého zarovnání histogramu.

Histogramy

Histogramy, které potřebujeme, jsou spojeny s CurrencyKey sloupec na každé spojené tabulce. Na nové kopii databáze AdventureWorksDW jsou již existující statistiky pro větší FactResellerSales tabulky jsou založeny na vzorku. Abychom maximalizovali reprodukovatelnost a co nejvíce zjednodušili provádění podrobných výpočtů (a abychom se vyhnuli škálování), první věc, kterou uděláme, je obnovit statistiky pomocí úplného skenování:

UPDATE STATISTICS dbo.FactCurrencyRate WITH FULLSCAN;
UPDATE STATISTICS dbo.FactResellerSales WITH FULLSCAN;

Výhodou těchto tabulek je vytvoření malého a jednoduchého maxdiff histogramy:

DBCC SHOW_STATISTICS
    (FactResellerSales, CurrencyKey)
WITH HISTOGRAM;
 
DBCC SHOW_STATISTICS
    (FactCurrencyRate, [PK_FactCurrencyRate_CurrencyKey_DateKey])
WITH HISTOGRAM;

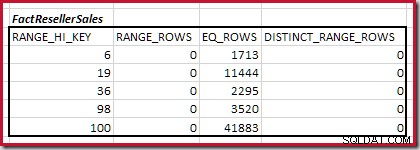
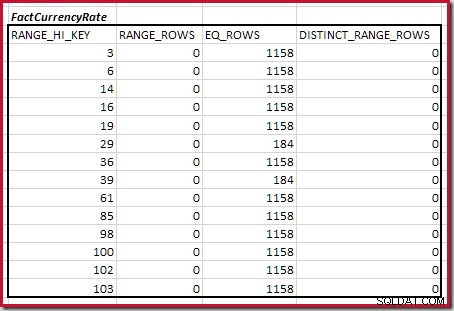
Kombinace minimálních kroků histogramu shody

První krok v hrubém zarovnání výpočet má najít příspěvek ke kardinalitě spojení poskytnutý nejnižším krokem shodného histogramu. Pro naše ukázkové histogramy je minimální hodnota shodného kroku na RANGE_HI_KEY = 6 :

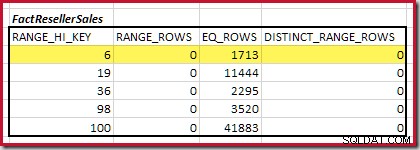
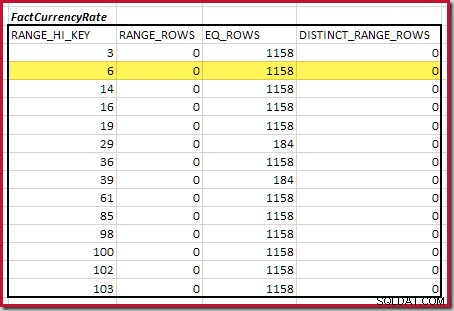
Odhadovaná mohutnost ekvijoinu pouze pro tento zvýrazněný krok je 1 713 * 1 158 =1 983 654 řádků .

Zbývající shodné kroky

Dále musíme identifikovat rozsah histogramu RANGE_HI_KEY kroky až na maximum pro možné shody equijoin. To zahrnuje posun vpřed od dříve nalezeného minima, dokud jednomu ze vstupů histogramu nedojdou řádky. Odpovídající rozsahy equijoin pro aktuální příklad jsou zvýrazněny níže:

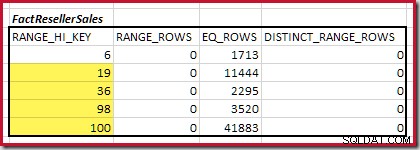
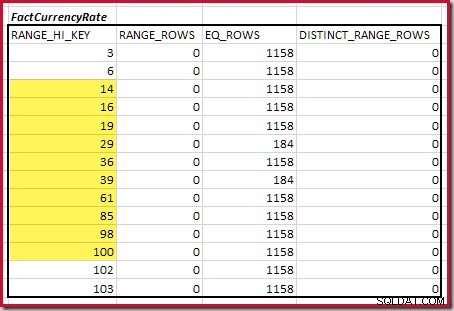
Tyto dva rozsahy představují zbývající řádky, u kterých lze očekávat, že přispějí k mohutnosti ekvijoinu.

Hrubý odhad na základě frekvence

Otázkou nyní je, jak provést hrubé odhad kardinality ekvijoinu zvýrazněných kroků pomocí dostupných informací.

Původní estimátor mohutnosti by provedl jemnozrnné postupné zarovnání histogramu pomocí lineární interpolace, posoudil příspěvek spojení každého kroku (stejně jako jsme to udělali pro minimální hodnotu kroku dříve) a sečetl každý příspěvek kroku, aby získal úplný odhad připojení. I když tento postup dává hodně intuitivní smysl, praktická zkušenost byla taková, že tento jemně zrnitý přístup zvýšil výpočetní režii a mohl přinést výsledky různé kvality.

Původní odhad měl jiný způsob, jak odhadnout kardinalitu spojení, když informace histogramu buď nebyly k dispozici, nebo byly heuristicky vyhodnoceny jako horší. Toto je známé jako odhad založený na frekvenci a používá následující definice:

• C – mohutnost (počet řádků)
• D – počet odlišných hodnot
• F – četnost (počet řádků) pro každou odlišnou hodnotu
• Poznámka C =D * F podle definice

Vliv ekvijunkce vztahů R1 a R2 na každou z těchto vlastností je znázorněn níže:

• F' =F1 * F2
• D' =MIN(D1; D2) – za předpokladu uzavření
• C' =D' * F' (opět podle definice)

Jsme po C', mohutnosti ekvijoinu. Nahrazení D' a F' ve vzorci a rozšíření:

• C' =D' * F'
• C' =MIN(D1; D2) * F1 * F2
• C' =MIN(D1 * F1 * F2; D2 * F1 * F2)
• nyní, protože C1 =D1 * F1 a C2 =D2 * F2:
• C' =MIN(C1 * F2, C2 * F1)
• nakonec, protože F =C/D (také podle definice):
• C' =MIN(C1 * C2 / D2; C2 * C1 / D1)

Všimněte si, že C1 * C2 je součin dvou vstupních mohutností (kartézské spojení), je jasné, že minimum těchto výrazů bude mít ten s vyšším počtem odlišných hodnot:

• C' =(C1 * C2) / MAX(D1; D2)

V případě, že se to všechno zdá trochu abstraktní, intuitivní způsob, jak přemýšlet o odhadu ekvijoin na základě frekvence, je zvážit, že každá odlišná hodnota z jednoho vztahu se spojí s počtem řádků (průměrná frekvence) v druhém vztahu. Pokud máme 5 různých hodnot na jedné straně a každá odlišná hodnota na druhé straně se objeví v průměru 3krát, rozumný (ale hrubý) odhad ekvijoin je 5 * 3 =15.

Není to tak široký štětec, jak by se mohlo zdát. Pamatujte, že výše uvedená mohutnost a odlišné hodnoty nepocházejí z celého vztahu, ale pouze z odpovídajících kroků nad minimem. Proto hrubý odhad mezi minimálními a maximálními hodnotami.

Výpočet frekvence

Každý z těchto parametrů můžeme získat ze zvýrazněných kroků histogramu.

• Kardinalita C je součet EQ_ROWS a RANGE_ROWS .
• Počet různých hodnot D je součet DISTINCT_RANGE_ROWS plus jeden za každý krok.

Mohutnost C1 odpovídající FactResellerSales kroky je součet zvýrazněných buněk:

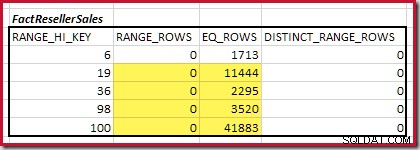
To dává C1 =59 142 řádky.

Neexistují žádné odlišné řádky rozsahu, takže jediné odlišné hodnoty pocházejí ze samotných čtyř kroků, takže D1 =4 .

Pro druhou tabulku:

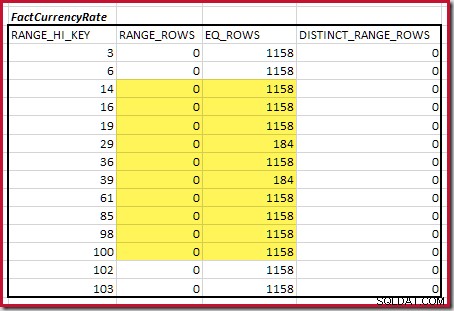
To dává C2 =9 632 . Opět zde nejsou žádné odlišné řádky rozsahu, takže odlišné hodnoty pocházejí z deseti kroků, D2 =10.

Dokončení odhadu Equijoin

Nyní máme všechna čísla, která potřebujeme pro rovnici ekvijoin:

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(59142 * 9632) / MAX(4; 10)
• C' =569655744 / 10
• C' =56 965 574,4

Pamatujte, že se jedná o příspěvek kroků histogramu nad minimální shodnou hranicí. Abychom dokončili odhad mohutnosti spojení, musíme přidat příspěvek z minimálních hodnot odpovídajících kroků, což bylo 1 713 * 1 158 =1 983 654 řádků.

Konečný odhad equijoin je tedy 56 965 574,4 + 1 983 654 =58 949 228,4 řádků neboli 58 949 200 na šest platných číslic.

Tento výsledek je potvrzen v odhadovaném plánu provádění pro zdrojový dotaz:

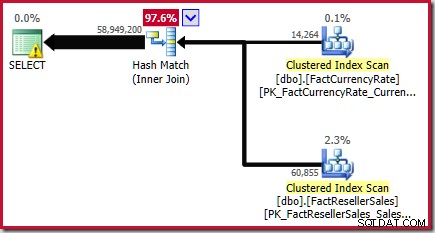
Jak je uvedeno v Bílé knize, není to příliš velký odhad. Skutečný počet řádků vrácených tímto dotazem je 70 470 090 . Odhad vytvořený původním ("starší") estimátorem mohutnosti – pomocí postupného zarovnání histogramu – je 70 470 100 řádků.

Lepší výsledky jsou často možné pomocí jemnější metody, ale pouze v případě, že statistiky velmi dobře reprezentují základní rozložení dat. Nejedná se pouze o udržování aktuálních statistik nebo používání úplné populace skenování. Algoritmus používaný ke sbalení informací do maximálně 201 kroků histogramu není dokonalý a v každém případě mnoho distribucí reálných dat takové věrnosti histogramu prostě není schopno. V průměru by lidé měli zjistit, že hrubší metoda poskytuje dokonale adekvátní odhady a větší stabilitu s novým CE.

Druhý příklad

To trochu navazuje na předchozí příklad a nevyžaduje stažení ukázkové databáze.

DROP TABLE IF EXISTS
    dbo.R1,
    dbo.R2;
 
CREATE TABLE dbo.R1 (n integer NOT NULL);
CREATE TABLE dbo.R2 (n integer NOT NULL);
 
INSERT dbo.R1
    (n)
VALUES
    (1), (2), (3), (4), (5), (6), (7), (8), (9), (10),
    (6), (6), (6), (6), (6), (6), (6), (6), (6), (6), 
    (6), (6), (6), (6), (6), (6), (6), (6), (6);
 
INSERT dbo.R2
    (n)
VALUES
    (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15),
    (10), (10);
 
CREATE STATISTICS stats_n ON dbo.R1 (n) WITH FULLSCAN;
CREATE STATISTICS stats_n ON dbo.R2 (n) WITH FULLSCAN;

Histogramy zobrazující odpovídající minimální kroky jsou:

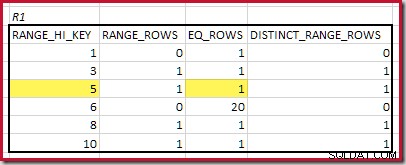
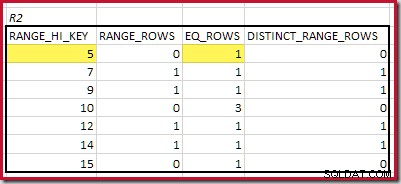
Nejnižší RANGE_HI_KEY která odpovídá je 5. Hodnota EQ_ROWS je 1 v obou, takže odhadovaná mohutnost ekvijoinu je 1 * 1 =1 řádek .

Nejvyšší shoda RANGE_HI_KEY je 10. Zvýraznění řádků histogramu R1 pro hrubý odhad založený na frekvenci:

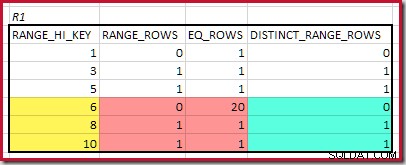
Součet EQ_ROWS a RANGE_ROWS dává C1 =24 . Počet samostatných řádků je 2 DISTINCT_RANGE_ROWS (odlišné hodnoty mezi kroky) plus 3 pro odlišné hodnoty spojené s každou hranicí kroku, takže D1 =5 .

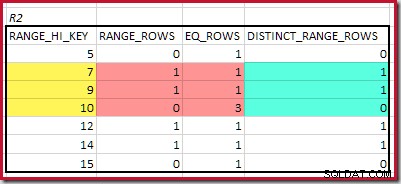
Pro R2, součet EQ_ROWS a RANGE_ROWS dává C2 =7 . Počet samostatných řádků je 2 DISTINCT_RANGE_ROWS (odlišné hodnoty mezi kroky) plus 3 pro různé hodnoty spojené s každou hranicí kroku, takže D2 =5 .

Odhad ekvijoin C' je:

• C' =(C1 * C2) / MAX(D1; D2)
• C' =(24 * 7) / 5
• C' =33,6

Přidávání do 1 řádku z minimální shody kroků dává celkový odhad 34,6 řádků pro equijoin:

SELECT
    R1.n,
    R2.n
FROM dbo.R1 AS R1
JOIN dbo.R2 AS R2
    ON R2.n = R1.n;

Odhadovaný plán realizace ukazuje odhad odpovídající našemu výpočtu:

To není úplně správné, ale „starší“ odhad mohutnosti na tom není lépe, odhaduje 15,25 řádků oproti 27 skutečným:

Pro úplné ošetření bychom také museli přidat konečný příspěvek z odpovídajících nulových kroků histogramu, ale to je neobvyklé pro ekvijoiny (které jsou obvykle psány tak, aby odmítaly hodnoty null) a pro čtenáře, kteří o to mají zájem, je to relativně jednoduché rozšíření.

Poslední myšlenky

Doufejme, že podrobnosti v článku vyplní pár mezer pro každého, kdo někdy přemýšlel o „hrubém zarovnání“. Všimněte si, že toto je jen jedna malá složka v odhadu mohutnosti. Existuje několik dalších důležitých konceptů a algoritmů používaných pro odhad spojení, zejména způsob, jakým jsou posuzovány predikáty bez spojení, a jak se zachází se složitějšími spojeními. Mnoho z opravdu důležitých částí je docela dobře pokryto v Bílé knize.