Geolokace velkého počtu příspěvků na základě IP adres. (880 000 řádků)

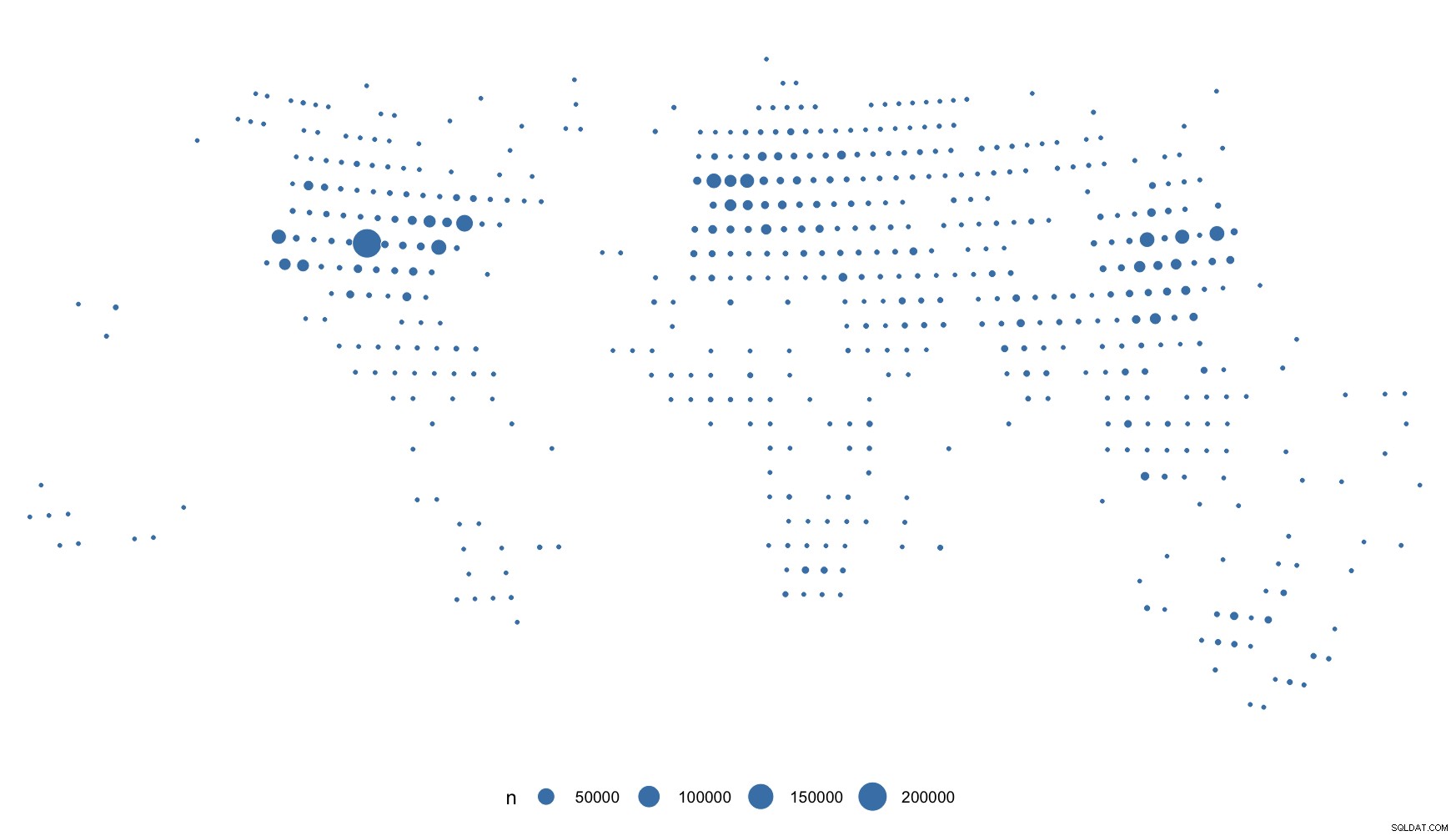
Vygenerujeme nějaké IP adresy, geolokalizujeme je a vykreslíme:

library(iptools)
library(rgeolocate)
library(tidyverse)

Vygenerujte milion (příliš rovnoměrně distribuovaných) náhodných adres IPv4:

ips <- ip_random(1000000)

A určete jejich polohu:

system.time(
  rgeolocate::maxmind(
    ips, "~/Data/GeoLite2-City.mmdb", c("longitude", "latitude")
  ) -> xdf
)
##    user  system elapsed 
##   5.016   0.131   5.217 

5s na 1m IPv4s. 👍🏼

Nyní kvůli uniformitě budou bubliny hloupě malé, takže jen pro tento příklad je trochu zaokrouhlíme:

xdf %>% 
  mutate(
    longitude = (longitude %/% 5) * 5,
    latitude = (latitude %/% 5) * 5
  ) %>%  
  count(longitude, latitude) -> pts

A vykreslete je:

ggplot(pts) +
  geom_point(
    aes(longitude, latitude, size = n), 
    shape=21, fill = "steelblue", color = "white", stroke=0.25
  ) +
  ggalt::coord_proj("+proj=wintri") +
  ggthemes::theme_map() +
  theme(legend.justification = "center") +
  theme(legend.position = "bottom")

Můžete vidět, co tím myslím "příliš uniformní". Ale máte „skutečné“ IPv4, takže byste měli být gtg.

Zvažte použití scale_size_area() , ale upřímně, zvažte, zda IPv4 na geografickou mapu vůbec nezakreslovat. Živím se výzkumem na internetu a tvrzení o přesnosti zanechávají mnoho přání. Z tohoto důvodu zřídka jdu pod atribuci na úrovni země (a platíme za „skutečná“ data).